Structural and Solid Mechanics
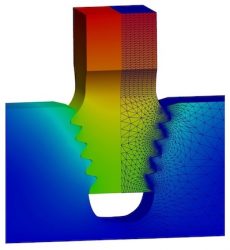
Beams, Shells, Membranes
The simulation of slender/thin structures requires specific numerical methods.
Our solution for you: Advanced beam, membrane and shell formulations, which are well suited for efficient computations of slender continua and can also be used for contact or multi-physics applications
Contact
Contact phenomena are frequently observable in nature as well as biological systems, and they are part of a variety of technical systems and machine components. To name but a few technical examples, contact plays a major role when considering gear-wheels, bearings, shafts, seals and car tires. In fact, there is merely an astoundingly low number of non-linear mechanical problems in which contact does not play any role at all. In many cases, there are further physical phenomena appearing in combination with contact, such as wear, heating, and lubrication. Another particularly challenging scenario is the combination of contact and fluid-structure interaction (FSI). All of the aforementioned physical complexities of contact problems render their numerical solution particularly challenging and unsolvable for traditional approaches.
Our solution for you: Advanced computational mortar methods, which always ensure a consistent load and motion transfer for any interface discretization. They are applicable to contact problems, also in combination with additional physical phenomena (e. g. wear ), and both so-called “wet contact” or “underwater contact”, respectively as well as so-called “dry contact”.
Material Modeling
Material modeling plays a crucial role in problems of structural mechanics. Both the functional relations between stress and strain and the correct choice of the corresponding material parameters are essential.
Our solution for you:
- Comprehensive libraries of materials
- Expertise in representing nonlinear hyperelastic and plastic material behavior
- Inclusion of anisotropy in various forms via fiber models
- Tailor-made algorithms to fit the parameters of material models to experimental measurements
Nonlinear Statics and Dynamics
The solution of non-linear problems involving large deformations and non-linear material models can be difficult. Especially when additional phenomena such as contact or interactions with other physical fields have to be taken into account, which is often the case.
Our solution for you:
- Comprehensive know-how for solving non-linear static and dynamic problems
- Our software enables us to consider all aforementioned complexities of the structural field, even in coupled problem scenarios.
Fluid Mechanics
The second major single mechanical field is the fluid field. Here, fluid encompasses both liquid and gaseous. A distinction is made between compressible and incompressible fluid flows as well as various flow regimes such as laminar, transitional and – usually of particular interest – turbulent. Moreover, multiple phases may occur in a flow problem, for instance, a liquid and a gaseous flow phase. A particular case in this context is cavitation, in which vapor-filled cavities can arise. In the following, we will briefly introduce our competencies with respect to the above.
Incompressible Flow
In many cases, incompressible flow can be assumed in fluid mechanics. For liquids, this assumption is indeed valid for the vast majority of flows. For flows of gases at a sufficiently low Mach number, which is frequently observed, it is also justified to consider the respective flow as incompressible.
Our solution for you: Advanced computational methods based on multiscale approaches for the simulation of incompressible flows
Variable-density flow
Variable-density flow at low Mach number is also often referred to as thermally coupled flow. Most combustion processes can be mathematically described by a variable-density formulation of the Navier-Stokes equations. Such a formulation poses additional challenges compared to, e. g., an incompressible formulation, since potentially large temperature differences and, as a consequence, large density differences must be considered.
Our solution for you: Advanced computational methods based on multiscale approaches to simulate variable-density flow across the full spectrum from laminar via transitional to the particularly challenging turbulent flow regime
Turbulence
The numerical simulation of turbulent flow is of paramount importance, since the majority of flows in nature and in technical applications are turbulent, such as the flows around a car or an airplane. Turbulent flow is a multiscale problem, characterized by a broad range of length and time scales. The computational cost for a complete resolution in the form of a direct numerical simulation (DNS) is (and will remain even in the foreseeable future) too high for almost all turbulent flows of engineering interest. Simulations based on Reynolds-Averaged Navier-Stokes (RANS) models are predominantly used in industry. However, RANS models typically require the tuning of various parameters for the problem at hand and thus lack general applicability.
Our solution for you: Advanced computational methods based on multiscale approaches for large-eddy simulation (LES) of turbulent flow, where the larger scales are resolved and the effect of the smaller scales on the larger scales is modeled
Multiphase flow
Multiphase flows appear in a variety of technical applications as well as in the natural environment. Cooling cycles, flows around ships, biological waste-water treatment, and groundwater flows are just a few examples. Compared to single-phase flow, multiphase flow poses additional challenges for computational methods, e. g., due to different physical properties of the individual phases as well as surface tension effects.
Our solution for you: Advanced computational methods in the form of extended Finite Element Method (XFEM) with multiscale approaches and Nitsche interface coupling to simulate multiphase flows across the entire spectrum from laminar to transitional up to particularly challenging turbulent flow regimes
Cavitation
Within flows, vapor cavities can evolve as well as decay due to locally different pressures. This process is referred to as cavitation. The number of such vapor bubbles in a flow can become very large. Furthermore, collisions between individual vapor bubbles may also occur. As a result, an adequate numerical modeling of cavitation is challenging.
Our solution for you: Advanced computational methods based on an Euler-Lagrange approach to simulate cavitation, where the flow is considered as a continuum in an Eulerian sense and the bubbles are considered as resolved phases in a Lagrangean sense
Thermomechanics
Continuum mechanics and thermodynamics are closely linked and can usually not be separated. Overall, the field is then commonly referred to as thermomechanical field. There are a variety of thermomechanical problems that can be studied using numerical methods. In general, these are the consideration of temporally varying temperature distributions in either solids or fluids. In the case of thermo-structure interaction, thermally induced strains can cause stresses and deformations can cause temperature variations. For variable-density flows temperature gradients can cause density variations, which can influence the flow. At the same time, the flow velocity can have a significant influence on the temperature distribution in the flow domain. In this context, the temperature is typically represented by a scalar quantity, which is subject to a corresponding transport equation.
Our solution for you: Advanced computational methods for thermo-structure interaction, thermo-fluid-structure interaction, and variable-density flow
Acoustics
Sound and its propagation are the subjects of the field of acoustics. Mathematically, the propagation of a wave such as a sound wave is described by a wave equation.
Our solution for you: Advanced computational methods in the form of so-called hybridizable discontinuous Galerkin (HDG) methods for the simulation of acoustic wave-propagation phenomena
Scalar transport: temperature and mass transport
Transport phenomena are part of many physical, chemical and biological processes. Temperature and mass transport may be distinguished. These transport phenomena, which are mathematically described by a scalar transport equation, can occur in solids as well as fluids. For more information on temperature transport, the reader is referred to thermomechanics.
Our solution for you: Advanced computational methods based on multiscale approaches for transport equations (Current projects within which we simulate temperature and mass transport can be found here and here.)
Electromagnetism
Electromagnetism describes the phenomenon of the formation of a magnetic field around a current-carrying conductor; it is caused by moving charges (current). Electromagnetism is mathematically described by Maxwell’s equations.
Our solution for you: Advanced computational methods in the form of so-called hybridizable discontinuous Galerkin (HDG) methods for the simulation of electromagnetic wave propagation phenomena
Biological fields
Aside from structural mechanics and transport phenomena, growth and remodeling processes are often particularly relevant in biological system. Exemplarily, the growth of biofilms and the pathological growth of vessels in the human body could be mentioned in this context.
Our solution for you: Advanced computational methods based on constraint mixture model formulations for growth and remodeling processes in computational models
Chemical (reactive) fields
We consider chemical fields in reactive or non-reactive form particularly in the context of two multiphysics problems, that is, electrochemistry and chemically reactive flows. Examples for chemically reactive flows are combustion, catalysis, and chemical vapor deposition, with combustion probably being the most widely known application. The reader is also referred to electrochemistry and combustion.
Our solution for you: Advanced computational methods based on multiscale approaches for the solution of transport equations governing the chemical field within electrochemical and combustion problems
